Area Of Parallelogram Programdownload Free Apps

Posted on |



Parallelogram Shape

How can this resource help teaching the area of a parallelogram? Differentiated activity sheets where children practice finding the area of parallelograms. Can I use these area of a parallelogram worksheets at home? Some parents may enjoy teaching the area of a parallelogram at home! This resource is easy to print off and use. Also, we prompt the user to enter the corresponding height of the parallelogram. We use the given formula to calculate the area of parallelogram and store it in a variable “area”. Finally, display the value to the user. Output: Height: 4 Base: 12 Area of the given Parallelogram is: 48.0. Also read, How to print deck of cards in Java.


a = side a lengths
b = side b lengths (base)
p = shorter diagonal length
q = longer diagonal length
h = height
A, B, C, D = corner angles
K = area
P = perimeter
π = pi = 3.1415926535898
√ = square root

Area Of A Parallelogram Examples

Calculator Use

Area Of Parallelogram Program Download Free Apps Download

Calculate certain variables of a parallelogram depending on the inputs provided. Calculations include side lengths, corner angles, diagonals, height, perimeter and area of parallelograms.

A parallelogram is a quadrilateral with opposite sides parallel. A parallelogram whose angles are all right angles is called a rectangle. And, a parallelogram whose angles are all right angels and whose sides are all equal is called a square. A rhombus (or diamond) is a parallelogram with all 4 sides equal length.

Units: Note that units of length are shown for convenience. They do not affect the calculations. The units are in place to give an indication of the order of the calculated results such as ft, ft2 or ft3. Any other base unit can be substituted. 8th grade ela benchmark test.

Parallelogram Formulas & Constraints

Corner Angles: A, B, C, D

  • A = C
  • B = D
  • A + B = 180° = π radians
  • for a parallelogram that is not a rectangle or square,
    • 0 < A< 90° (0 < A < π/2),
    • 90° < B < 180° (π/2 < B < π)

Area: K

with A and B in radians,

Area Of Parallelogram From Points

K = bh = ab sin(A) = ab sin(B)

Height: h

Area Of Parallelogram With Coordinates

h = a sin(A) = a sin(B)

Apps

Diagonals: p, q

Area Of Parallelogram Programdownload Free Apps
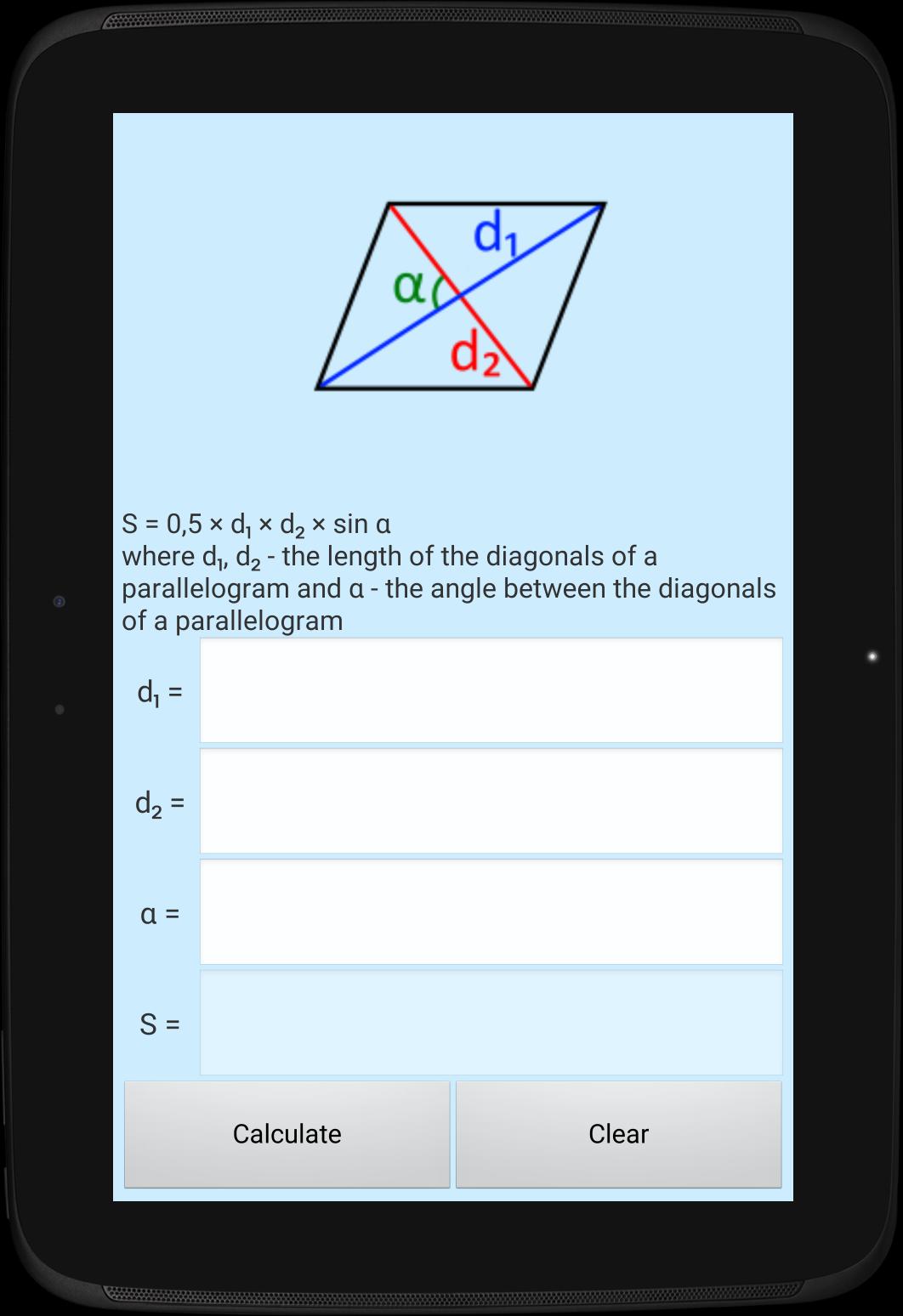
  • p = √( a2 + b2 - 2ab cos(A) ) = √( a2 + b2 + 2ab cos(B) )
  • q = √( a2 + b2 + 2ab cos(A) ) = √( a2 + b2 - 2ab cos(B) )
  • p2 + q2 = 2(a2 + b2)

Perimeter: P

P = 2a + 2b

Parallelogram Area Problems

Parallelogram Calculations:

The following formulas, based on those above, are used within this calculator for the selected calculation choices.

  • Calculate B, C, D | Given A
    Given angle A calculate angles B, C and D
    • B = 180° - A
    • C = A
    • D = B
  • Calculate A, C, D | Given B
    Given angle B calculate angles A, C and D
    • A = 180° - B
    • C = A
    • D = B
  • Calculate h, B, C, D | Given A, a
    Given angle A and side a calculate height and angles B, C and D
    • h = a sin(A)
    • B = 180° - A
    • C = A
    • D = B
  • Calculate a, B, C, D | Given A, h
    Given angle A and height calculate side a and angles B, C and D
    • a = h / sin(A)
    • B = 180° - A
    • C = A
    • D = B
  • Calculate b | Given P, a
    Given the perimeter and side a calculate side b
    • b = (P - 2a) / 2
  • Calculate a | Given P, b
    Given the perimeter and side b calculate side a
    • a = (P - 2b) / 2
  • Calculate P | Given a, b
    Given side lengths calculate the perimeter
    • P = 2a + 2b
  • Calculate h | Given K, b
    Given area and side b calculate height
    • h = K / b
  • Calculate b | Given K, h
    Given area and height calculate side b
    • b = K / h
  • Calculate K | Given b, h
    Given side b and height calculate area
    • K = bh
  • Calculate B, p, q, h, P, K | Given a, b, A
    Given side lengths and angle A calculate the diagonals, perimeter, height, area and angles B, C and D
    • p = √( a2 + b2 - 2ab cos(A) )
    • q = √( a2 + b2 + 2ab cos(A) )
    • P = 2a + 2b
    • h = a sin(A)
    • K = bh
    • B = 180° - A
    • C = A
    • D = B
  • Calculate A, B, q, h, P, K | Given a, b, p
    Given side lengths and diagonal p calculate diagonal q, perimeter, height, area and angles A, B, C and D
    • A = arccos( (p2 - a2 - b2) / (-2ab) )
    • q = √( a2 + b2 + 2ab cos(A) )
    • h = a sin(A)
    • P = 2a + 2b
    • K = ab sin(A)
    • B = 180° - A
    • C = A
    • D = B
  • Calculate A, B, p, h, P, K | Given a, b, q
    Given side lengths and diagonal q calculate diagonal p, perimeter, height, area and angles A, B, C and D
    • A = arccos( (q2 - a2 - b2) / (2ab) )
    • p = √( a2 + b2 - 2ab cos(A) )
    • h = a sin(A)
    • P = 2a + 2b
    • K = ab sin(A)
    • B = 180° - A
    • C = A
    • D = B
  • Calculate A, B, p, q, P, K | Given a, b, h
    Given side lengths and height calculate the diagonals, perimeter, area and angles A, B, C and D
    • A = arcsin(h/a)
    • p = √( a2 + b2 - 2ab cos(A) )
    • q = √( a2 + b2 + 2ab cos(A) )
    • P = 2a + 2b
    • K = ab sin(A)
    • B = 180° - A
    • C = A
    • D = B
  • Calculate A, B, p, q, h, P | Given a, b, K
    Given side lengths and area calculate the diagonals, perimeter, height and angles A, B, C and D
    • A = arcsin(K/ab)
    • p = √( a2 + b2 - 2ab cos(A) )
    • q = √( a2 + b2 + 2ab cos(A) )
    • h = a sin(A)
    • P = 2a + 2b
    • B = 180° - A
    • C = A
    • D = B
  • Calculate B, b, p, q, h, P | Given a, A, K
    Given side length a, angle A and area calculate the diagonals, perimeter, height, side length b and angles B, C and D
    • b = K / (a sin(A))
    • p = √( a2 + b2 - 2ab cos(A) )
    • q = √( a2 + b2 + 2ab cos(A) )
    • h = a sin(A)
    • P = 2a + 2b
    • B = 180° - A
    • C = A
    • D = B
  • Calculate B, a, p, q, h, P | Given b, A, K
    Given side length b, angle A and area calculate the diagonals, perimeter, height, side length a and angles B, C and D
    • a = K / (b sin(A))
    • p = √( a2 + b2 - 2ab cos(A) )
    • q = √( a2 + b2 + 2ab cos(A) )
    • h = a sin(A)
    • P = 2a + 2b
    • B = 180° - A
    • C = A
    • D = B
  • Calculate A, B, b, h, P, K | Given a, p, q
    Given side length a and the diagonals calculate the perimeter, height, area, side length b and angles A, B, C and D
    • b = √( (p2 + q2 - 2a2) / 2 )
    • A = arccos( (q2 - a2 - b2) / (2ab) )
    • h = a sin(A)
    • P = 2a + 2b
    • K = ab sin(A)
    • B = 180° - A
    • C = A
    • D = B
  • Calculate A, B, a, h, P, K | Given b, p, q
    Given side length b and the diagonals calculate the perimeter, height, area, side length a and angles A, B, C and D
    • a = √( (p2 + q2 - 2b2) / 2 )
    • A = arccos( (q2 - a2 - b2) / (2ab) )
    • h = a sin(A)
    • P = 2a + 2b
    • K = ab sin(A)
    • B = 180° - A
    • C = A
    • D = B

References

Zwillinger, Daniel (Editor-in-Chief). CRC Standard Mathematical Tables and Formulae, 31st Edition New York, NY: CRC Press, p. 322, 2003.

Math Forum: Ask Dr. Math FAQ: Quadrilateral Formulas (http://mathforum.org/)

Weisstein, Eric W. 'Parallelogram.' From MathWorld--A Wolfram Web Resource. Parallelogram.